Computing the load-dependent stiffness and damping matrices of journal bearings
Compared to rolling bearings, hydrodynamic journal bearings show a significantly stronger nonlinear dependance on various operating parameters. If these operating parameters change as during a run-up for example, the stiffness and the damping of the journal bearings change according to the continuous change of the rotation speed.
The Reynolds equation, which represents the core differential equation for the hydrodynamic lubrication theory, describes the location and time dependance of the hydrodynamic pressure in the bearing. In a few cases like for short circular cylindrical bearings, closed solutions of this equation exist for suitable boundary conditions. For this task ISMB developed the software ISMBear, which is based on MATLAB.
ISMBear computes the static position of the shaft within the bearing gap depending on the geometric dimensions of the jounal bearing and on various operating parameters like the rotation speed and the viscosity of the lubricant. ISMBear computes and visualizes the static position as well as the linearized stiffness and damping matrices.
ISMBear is able to compute the stiffness and damping matrices for any operating condition. Thus the relevant dynamic properties of the journal bearings can be obtained during a complete run-up.
These data we use for instance for rotor dynamic simulations of power drive lines during their run-up. For this purpose, the stiffness and damping matrices are computed with ISMBear for various operating conditions. These data are exported to our inhouse rotor dynamic simulation software RODY which additionally considers the dynamic properties of the rotor and, if required, also of the housing. RODY creates frequency and damping maps of the speed dependent vibration modes, calculates frequency response functions (FRFs) due to arbitrary excitations and operating deflection shapes (ODS).
Our specialists are always at your disposal to flexibly respond to your respective requirements and wishes.
Dr. Michael Elbs, Managing Director

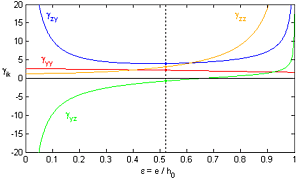
Dimensionless stiffness depending on the static displacement ε
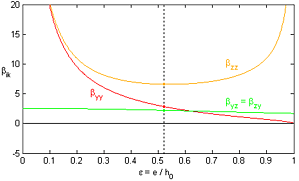
Dimensionless damping depending on the static displacement ε
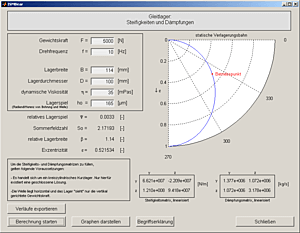
ISMBear visualizes the static position of the shaft within the bearing gap which depends on various parameters

